Caso de estudio

Para el sistema mostrado en la figura $\ref{caso}$. Se busca lo siguiente:

• Ecuaciones que gobiernan el comportamiento dinámico del sistema.
• Ecuaciones linealizadas para el equilibrio $\varphi_{1}=\varphi_{2}=0$
• Valores críticos de $P$ que desestabilizan al modelo linealizado (tomar $m_{1}=m_{2}$, $l_{1}=l_{2}$, $k_{1}=k_{2}$).
• Añadir amortiguamiento lineal en las uniones $c_{1}$ y $c_{2}$
• Estudiar numéricamente el efecto sobre la estabilidad del sistema.

Solución del caso de estudio

El caso de estudio es el sistema de Ziegler mostrado en la figura 1.

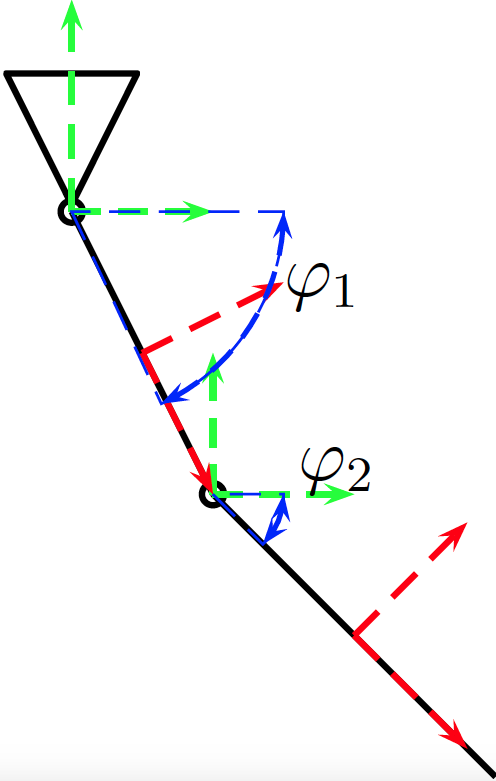
*Fig1: Caso de Estudio*

Para obtener la ecuación de movimiento utilizamos un método energético como la ecuación de Lagrange:

$$\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{q_i} }-\frac{\partial L}{\partial q_i}&=&Q_{g} \label{lagrange} \\ L &=&T-U \end{eqnarray}$$

La energía cinética del sistema es:

$$\begin{eqnarray} T &=&\frac{1}{2}J_{1}\dot{\varphi}_{1}^{2}+\frac{1}{2}m_{2} \dot{\textbf{r}}_{g2} \cdot \dot{\textbf{r}}_{g2}+ \frac{1}{2}J_{cg2}\dot{\varphi}_{2}^{2} \end{eqnarray}$$

En donde $J_{1}=\frac{1}{3}m_{1}L^{2}$ y $J_{cg2}=\frac{1}{12}mL^{2}$

Mientras que la posición del centro de gravedad del cuerpo 2 en cada instante es:

$$\begin{eqnarray} \textbf{r}_{g2}&=&\left (L_{1}\cos \varphi _{1} +\frac{L_{2}}{2}\cos \varphi_{2}\right )\textbf{i}+ \left (L_{1}\sin \varphi_{1} +\frac{L_{2}}{2}\sin \varphi_{2}\right )\textbf{j} \end{eqnarray}$$

De tal forma que la velocidad del centro de gravedad de la barra 2 sería:

$$\begin{eqnarray} \dot{\textbf{r}}_{g2}&=&-\left ( L_{1}\dot{\varphi}_{1}\sin \varphi_{1}+\frac{L_{2}}{2}\dot{\varphi}_{2}\sin \varphi_{2}\right )\textbf{i}+ \left (L_{1}\dot{\varphi}_{1}\cos \varphi _{1}+\frac{L_{2}}{2}\dot{\varphi}_{2}\cos \varphi_{2}\right )\textbf{j} \end{eqnarray}$$

Como $m_{1}=m_{2}$, $L_{1}=L_{2}$, $c_{1}=c_{2}$, entonces:

$$\begin{eqnarray} \dot{\textbf{r}}_{g2} \cdot \dot{\textbf{r}}_{g2}&=&L^{2}\dot{\varphi}_{1}^{2}\sin ^{2}\varphi_{1}+L^{2}\dot{\varphi}_{1}\dot{\varphi}_{2}\sin \varphi_{1}\sin \varphi_{2}+\frac{L^{2}}{4}\dot{\varphi}_{2}^{2}\sin ^{2}\varphi_{2}+L^{2}\dot{\varphi}_{1}^{2}\cos ^{2}\varphi_{1}\cdots \nonumber \\ && + L^{2}\dot{\varphi}_{1}\dot{\varphi}_{2}\cos \varphi_{1}\cos \varphi_{2}+\frac{L^{2}}{4}\dot{\varphi}_{2}^{2}\cos ^{2}\varphi_{2}\nonumber \\ \dot{\textbf{r}}_{g2} \cdot \dot{\textbf{r}}_{g2}&=&L^{2}\dot{\varphi}_{1}^{2}+L^{2}\dot{\varphi}_{1}\dot{\varphi}_{2}\cos (\varphi_{1}-\varphi_{2})+\frac{L^{2}}{4}\dot{\varphi}_{2}^{2} \end{eqnarray}$$ $$\begin{eqnarray} T &=&\frac{1}{6}m L^{2}\dot{\varphi}_{1}^{2}+\frac{1}{2}m\left (L^{2}\dot{\varphi}_{1}^{2}+L^{2}\dot{\varphi}_{1}\dot{\varphi}_{2}\cos (\varphi_{1}-\varphi_{2})+\frac{L^{2}}{4}\dot{\varphi}_{2}^{2}\right )+\frac{1}{24}mL^{2}\dot{\varphi}_{2}^{2} \end{eqnarray}$$

Mientras que para la energía potencial se tiene:

$$\begin{eqnarray} V&=&\frac{1}{2}k\varphi_{1}^{2}+\frac{1}{2}k\varphi_{2}^{2}\\ \end{eqnarray}$$

Carga Generalizada

Para calcular la fuerza generalizada producida por la carga $P$ se implementa el principio de los trabajos virtuales:

$$\begin{eqnarray} \delta \textbf{W} &=&\textbf{P}\delta \textbf{r}_{g} \end{eqnarray}$$ $$\begin{eqnarray} \delta \textbf{r}_{g}&=&\left [ \begin{array}{c} -(L_{1}\delta \varphi_{1} \sin \varphi_{1}+ L_{2}\delta \varphi_{2} \sin \varphi_{2}) \\ L_{1}\delta \varphi_{1} \cos \varphi_{1}+ L_{2}\delta \varphi_{2} \cos \varphi_{2} \end{array} \right ] \end{eqnarray}$$ $$\begin{eqnarray} \textbf{P} &=&\left [ \begin{array}{c} -P\cos \varphi_{2}\\ -P\sin \varphi_{2} \end{array} \right ] \end{eqnarray}$$

Entonces:

$$\begin{eqnarray} \delta \textbf{W}&=&\left [ \begin{array}{cc} -P\cos \varphi_{2} & -P\sin \varphi_{2} \end{array} \right ] \left [ \begin{array}{c} -(L_{1}\delta \varphi_{1} \sin \varphi_{1}+ L_{2}\delta \varphi_{2} \sin \varphi_{2}) \\ L_{1}\delta \varphi_{1} \cos \varphi_{1}+ L_{2}\delta \varphi_{2} \cos \varphi_{2} \end{array} \right ]\nonumber \\ &=&PL_{1}[\cos \varphi_{2}\sin \varphi_{1}-\sin \varphi_{2}\cos \varphi_{1}]\delta \varphi_{1}+PL_{2}[\cos \varphi_{2}\sin \varphi_{2}-\cos \varphi_{2} \sin \varphi_{2}]\delta \varphi_{2} \label{momentos} \end{eqnarray}$$

De tal forma que a partir de la ecuación \eqref{momentos} podemos deducir lo siguiente:

$$\begin{eqnarray} Q_{1}&=&PL[\cos \varphi_{2}\sin \varphi_{1}-\sin \varphi_{2}\cos \varphi_{1}]\\ Q_{2}&=&PL[\cos \varphi_{2}\sin \varphi_{2}-\cos \varphi_{2} \sin \varphi_{2}] \end{eqnarray}$$

Ecuaciones de movimiento

Las ecuaciones de movimiento del sistema a partir de la ecuación \eqref{lagrange} son:

$$\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{\varphi}_{1} }-\frac{\partial L}{\partial \varphi _{1}}&=&Q_{1} \\ \frac{4}{3}mL^{2}\ddot{\varphi}_{1}+\frac{1}{2}mL^{2}\ddot{\varphi}_{2}\cos (\varphi_{1}-\varphi_{2})\dots&& \nonumber \\+\frac{1}{2}mL^{2}\dot{\varphi}_{2}^{2}\sin (\varphi_{1} -\varphi_{2})+k\varphi_{1}&=&PL[\cos \varphi_{2}\sin \varphi_{1}-\sin \varphi_{2}\cos \varphi_{1}] \end{eqnarray}$$

Mientras que la segunda ecuación sería:

$$\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial \dot{\varphi}_{2} }-\frac{\partial L}{\partial \varphi_{2}}&=&Q_{2} \\ \frac{1}{2}mL^{2}\ddot{\varphi}_{1}\cos (\varphi_{1}-\varphi_{2})-\frac{1}{2}mL^{2}\dot{\varphi}_{1}^{2}\sin (\varphi_{1}-\varphi_{2})+\frac{1}{3}mL^{2}\ddot{\varphi}_{2}+k\varphi_{2}&=&0 \end{eqnarray}$$

Resumiendo, las ecuaciones que gobiernan el movimiento del sistema serían las siguientes:

$$\begin{eqnarray} \frac{4}{3}mL^{2}\ddot{\varphi}_{1}+\frac{1}{2}mL^{2}\ddot{\varphi}_{2}\cos (\varphi_{1}-\varphi_{2})+\frac{1}{2}mL^{2}\dot{\varphi}_{2}^{2}\sin (\varphi_{1} -\varphi_{2})+k\varphi_{1}&=&PL\sin (\varphi_{1}-\varphi_{2}) \label{ecmov1}\\ \frac{1}{2}mL^{2}\ddot{\varphi}_{1}\cos (\varphi_{1}-\varphi_{2})-\frac{1}{2}mL^{2}\dot{\varphi}_{1}^{2}\sin (\varphi_{1}-\varphi_{2})+\frac{1}{3}mL^{2}\ddot{\varphi}_{2}+k\varphi_{2}&=&0 \label{ecmov2} \end{eqnarray}$$

Ecuaciones de equilibrio linealizadas

Las ecuaciones \eqref{ecmov1} y \eqref{ecmov2} representan las ecuaciones de movimiento del sistema NO lineales. Si ahora linealizamos respecto a la posición $(\varphi_{1},\varphi_{2})=(0,0)$. Obtenemos lo siguiente:

$$\begin{eqnarray} \frac{4}{3}mL^{2}\ddot{\varphi}_{1}+\frac{1}{2}mL^{2}\ddot{\varphi}_{2}+k\varphi_{1}&=&PL(\varphi_{1}-\varphi_{2}) \label{ecmov1lin}\\ \frac{1}{2}mL^{2}\ddot{\varphi}_{1}+\frac{1}{3}mL^{2}\ddot{\varphi}_{2}+k\varphi_{2}&=&0 \label{ecmov2lin} \end{eqnarray}$$

Analisis de estabilidad

El sistema en forma matricial sería el siguiente:

$$\begin{eqnarray} \left [ \begin{array}{cc} \frac{4}{3}mL^{2}&\frac{1}{2}mL^{2}\\ \frac{1}{2}mL^{2}&\frac{1}{3}mL^{2} \end{array} \right ] \left [ \begin{array}{c} \ddot{\varphi}_{1}\\\ddot{\varphi}_{2} \end{array} \right ]+ \left [ \begin{array}{cc} k-PL&PL\\ 0&k \end{array} \right ] \left [ \begin{array}{c} \varphi_{1}\\ \varphi_{2} \end{array} \right ] &=& \left [ \begin{array}{c} 0\\0 \end{array} \right ] \end{eqnarray}$$

Si descomponemos la matriz en matriz simétrica y antisimétrica:

$$\begin{eqnarray} \left [ \begin{array}{cc} \frac{4}{3}mL^{2}&\frac{1}{2}mL^{2}\\ \frac{1}{2}mL^{2}&\frac{1}{3}mL^{2} \end{array} \right ] \left [ \begin{array}{c} \ddot{\varphi}_{1}\\\ddot{\varphi}_{2} \end{array} \right ]+ \left [ \begin{array}{cc} k-PL&\frac{1}{2}PL\\ \frac{1}{2}PL&k \end{array} \right ] \left [ \begin{array}{c} \varphi_{1}\\ \varphi_{2} \end{array} \right ] + \left [ \begin{array}{cc} 0&\frac{1}{2}PL\\ -\frac{1}{2}PL&0 \end{array} \right ] \left [ \begin{array}{c} \varphi_{1}\\ \varphi_{2} \end{array} \right ] &=& \left [ \begin{array}{c} 0\\0 \end{array} \right ] \end{eqnarray}$$

De tal forma que el sistema de ecuaciones quedaría de la siguiente forma:

$$\begin{eqnarray} \left [ LL^{T} \right ] \left [ \begin{array}{c} \ddot{\varphi}_{1}\\\ddot{\varphi}_{2} \end{array} \right ]+ \left [ K \right ] \left [ \begin{array}{c} \varphi_{1}\\ \varphi_{2} \end{array} \right ] + \left [ P \right ] \left [ \begin{array}{c} \varphi_{1}\\ \varphi_{2} \end{array} \right ] &=& \left [ \begin{array}{c} 0\\0 \end{array} \right ] \\ \left [ L^{-1}L \right ] \left [ \begin{array}{c} \ddot{u}\\\ddot{v} \end{array} \right ]+ L^{-1} \left [ K \right ] \left(L^{T}\right )^{-1} \left [ \begin{array}{c} u\\ v \end{array} \right ] + L^{-1} \left [ P \right ] \left(L^{T}\right )^{-1} \left [ \begin{array}{c} u\\ v \end{array} \right ] &=& \left [ \begin{array}{c} 0\\0 \end{array} \right ] \\ \left [ \begin{array}{c} \ddot{u}\\\ddot{v} \end{array} \right ]+ L^{-1} \left [ K \right ] \left(L^{T}\right )^{-1} \left [ \begin{array}{c} u\\ v \end{array} \right ] + L^{-1} \left [ P \right ] \left(L^{T}\right )^{-1} \left [ \begin{array}{c} u\\ v \end{array} \right ] &=& \left [ \begin{array}{c} 0\\0 \end{array} \right ] \end{eqnarray}$$

Para una solución de la forma $\textbf{u}=\textbf{U}e^{\lambda t}$:

$$\begin{eqnarray} \left [ \lambda ^{2}\textbf{I}+ \textbf{K}+ \textbf{P} \right ]\left [ \begin{array}{c} u\\v \end{array}\right ]&=&\left [ \begin{array}{c} 0\\0 \end{array}\right ] \end{eqnarray}$$

Resolviendo el problema de valores característicos, los eigenvalores serían:

$$\begin{eqnarray} \lambda ^{2}_{1,2}&=& \left[ \begin {array}{c} 1/12\,{\frac { \left( -10\,k+5\,PL+\sqrt {25 \,{P}^{2}{L}^{2}-72\,PLk+72\,{k}^{2}} \right) m{L}^{2}}{k \left( -k+PL \right) }}\\ 1/12\,{\frac { \left( -10\,k+5\,PL- \sqrt {25\,{P}^{2}{L}^{2}-72\,PLk+72\,{k}^{2}} \right) m{L}^{2}}{k \left( -k+PL \right) }}\end {array} \right] \label{eigen6} \end{eqnarray}$$

A partir de las expresiones para los valores de $\lambda$ en las ecuaciones \eqref{eigen6} se puede concluir que el sistema se vuelve inestable para valores de $P>100$ esto utilizando valores de $k=100$, $m=0.3$ y $L=1$. Para comprobar esta conclusión se procedió a resolver numéricamente el sistema de ecuaciones linealizadas. Los resultados son mostrados en las figuras \ref{fig1}, \ref{fig2}, \ref{fig3} y \ref{fig4}.

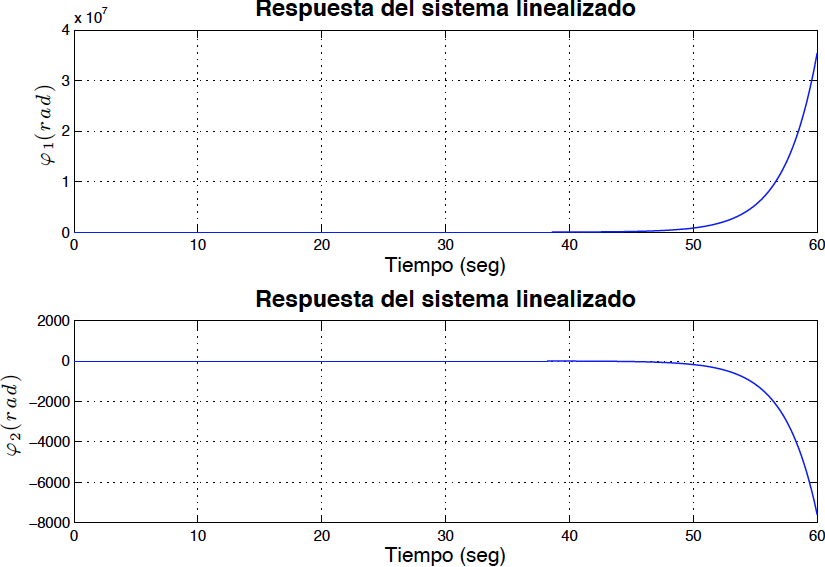
*Fig2: Respuesta del sistema linealizado para $P=100.1$ sin amortiguamiento (Inestable)*

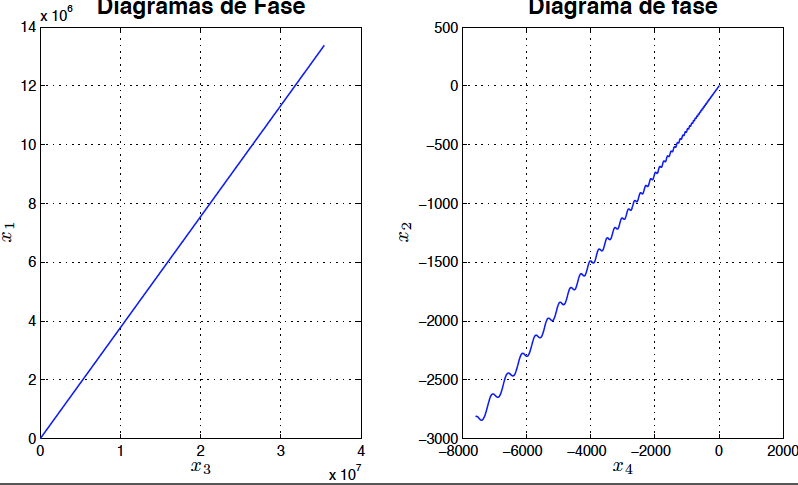
*Fig3: Diagrama de fase del sistema linealizado para $P=100.1$ sin amortiguamiento (Inestable)*

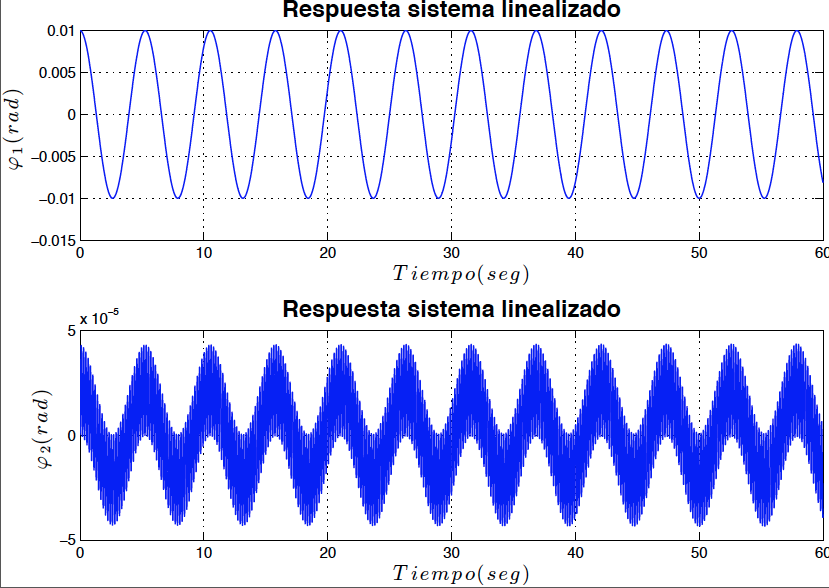
*Fig4: Respuesta del sistema linealizado para $P=99$ sin amortiguamiento (Marginalmente estable)*

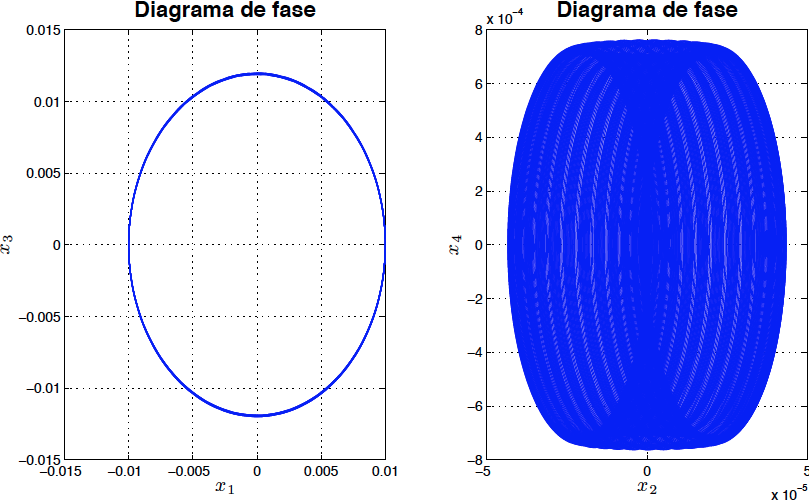
*Fig5: Diagrama de fase del sistema linealizado para $P=99$ sin amortiguamiento (Marginalmente estable)*

Sistema con amortiguamiento

Para el caso en el cual se añada amortiguamiento al sistema $c=0.40$, las ecuaciones que gobiernan el movimiento serían las siguientes:

$$\begin{eqnarray} \frac{4}{3}mL^{2}\ddot{\varphi}_{1}+\frac{1}{2}mL^{2}\ddot{\varphi}_{2}\cos (\varphi _{1}-\varphi _{2})+\frac{1}{2}mL^{2}\dot{\varphi}_{2}^{2}\sin (\varphi _{1} -\varphi _{2})+k\varphi _{1}+c\dot{\varphi}_{1}&=&PL\sin (\varphi _{1}-\varphi _{2}) \label{ecmov11}\\ \frac{1}{2}mL^{2}\ddot{\varphi}_{1}\cos (\varphi _{1}-\varphi _{2})-\frac{1}{2}mL^{2}\dot{\varphi}_{1}^{2}\sin (\varphi _{1}-\varphi _{2})+\frac{1}{3}mL^{2}\ddot{\varphi}_{2}+k\varphi _{2}+c\dot{\varphi}_{2}&=&0 \label{ecmov22} \end{eqnarray}$$

Resolviendo las ecuaciones \eqref{ecmov11} y \eqref{ecmov22} numéricamente utilizando MATLAB, los resultados son los mostrados en las figuras \ref{fig5} y \ref{fig6}

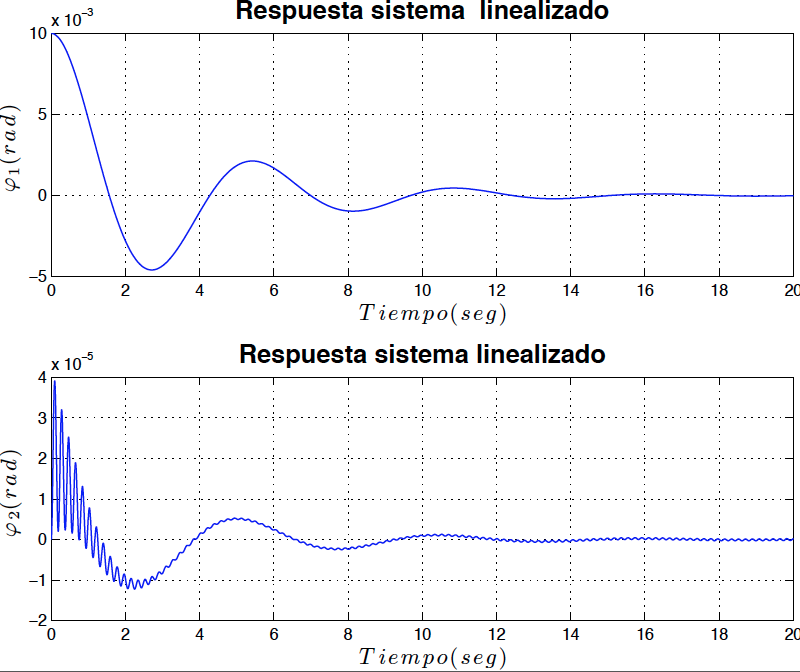
*Fig6: Respuesta del sistema linealizado para $P=99$ con amortiguamiento (asintóticamente estable)*

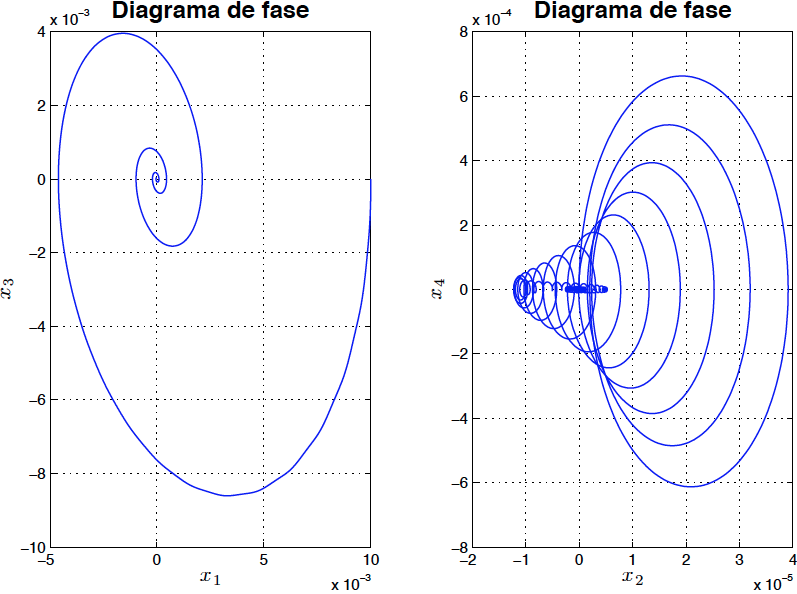
*Fig7: Diagrama de fase del sistema linealizado para $P=99$ con amortiguamiento (asintóticamente estable)*

Sistema no lineal

Para analizar la respuesta del sistema ante las no linealidades el sistema de ecuaciones no lineales \eqref{ecmov11} y \eqref{ecmov22} se resolvió utilizando la función ODE45 de Matlab. Los resultados son mostrados en las figuras \ref{fig7} y \ref{fig8}.\[300cm]

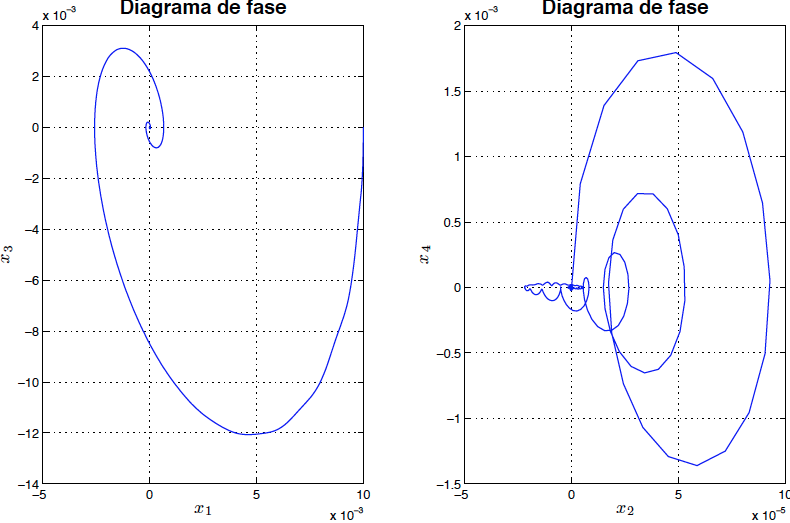
*Fig8: Diagrama de fase del sistema no linealizado para $P=99$ con amortiguamiento (asintóticamente estable)*

*Fig9: Diagrama de fase del sistema no linealizado para $P=99$ con amortiguamiento (asintóticamente estable)*

Anexos

Código utilizado en MATLAB para resolver el sistema de ecuaciones \eqref{ecmov1lin}, \eqref{ecmov2lin}, \eqref{ecmov11} y \eqref{ecmov22}

Fichero Principal

Sistema lineal

Sistema no lineal

---

Método Newton-Raphson por Jorge De La Cruz se distribuye bajo una Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

---